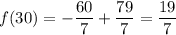Question

Alana and Kelsa are training for a marathon. To prepare for this marathon they have been training and tracking their progress periodically.

In the first week of training Alana ran an average of 14 minutes per mile. Later, in week nine of training she ran an average of 10 minutes per mile.

In the first week of training Kelsa ran an average of 11 minutes per mile. Later, in week eight of training she ran an average of 9 minutes per mile.

Assuming Alana and Kelsa continue to train and improve their times at the same rate your task it to determine which week they will have the same average minutes per mile. We will assume that the relationship is linear as they will be training for a maximum of 43 weeks. To complete this task follow the steps below.

1. Determine the equation of a line in standard form that represents Alana's training progress. Her progress corresponds to the points (1,14) and (9,10).

2. Determine the equation of a line in standard form that represents Kelsa's training progress. Her progress corresponds to the points (1,11) and (8,9).

3. Solve the system of equations (show all work)

4. In which week will Alana and Kelsa have the same average minute per mile?

5. If Alana and Kelsa continue to train until week 30, what will their times be?

Answer 1

The exercise is already scheduled, so we just follow the instruction:

1: Given two points
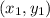`(x_1,y_1)` and
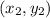`(x_2,y_2)`, the equation of the line passing through the two points is given by

`(x-x_1)/(x_2-x_1)=(y-y_1)/(y_2-y_1)`

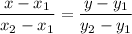
In your case, we have

`(x-1)/(9-1)=(y-14)/(10-14) \iff (x-1)/(8)=(y-14)/(-4) \iff x-1=28-2y`

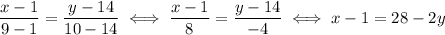
To put this equation into standard form, we have

`x-1=28-2y \iff 2y = -x+1+28 \iff y = -(x)/(2)+(29)/(2)`

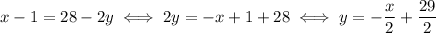
2: By the exact same logic, the line that represents Kelsa's training progress is given by

`(x-1)/(8-1)=(y-11)/(9-11) \iff (x-1)/(7)=(y-11)/(-2) \iff 2(x-1)=-7(y-11)`

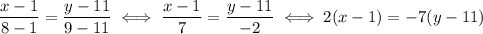
Solving for y yields

`2(x-1)=-7(y-11) \iff 2x-2=-7y+77 \iff 7y=-2x+2+79`

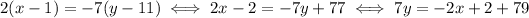
and finally

`y=(-2x)/(7)+(79)/(7)`

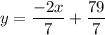
3: We have the following system:

`\begin{cases}y = -(x)/(2)+(29)/(2)\\y=(-2x)/(7)+(79)/(7)\end{cases}`

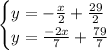
Since both equations are solved for y, we deduce that the two right hand sides must be equal:

`-(x)/(2)+(29)/(2)=(-2x)/(7)+(79)/(7)`

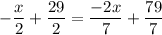
Multiply both equations by 14 to get rid of the denominators:

`-7x+203=-4x+158 \iff 3x=45 \iff x=15`

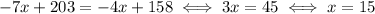
Plug this value for x in one of the equations:

`y = -(15)/(2)+(29)/(2)=7`

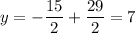
4: Since x represents the number of weeks, and x = 7 is the solution of the system, after 7 weeks they will habe the same average minute per mile

5: We have the equations that represent the times of the two girls, depending on time. So, we simply have to plug x=30 in the equations to get the times after 30 weeks: for Alana we have

`f(x) = -(x)/(2)+(29)/(2)\implies f(30)=-(30)/(2)+(29)/(2)`

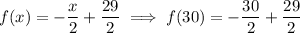
which evaluates to

`f(30)=-15+(29)/(2)=-(1)/(2)`

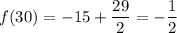
And for Kelsa we have

`f(x) = (-2x)/(7)+(79)/(7)\implies f(30)=(-2\cdot 30)/(7)+(79)/(7)`

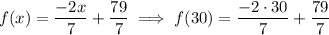
which evaluates to

`f(30)=-(60)/(7)+(79)/(7)=(19)/(7)`