Answer:
Maria and Josie working together can complete the work in= 1 hour and 20 minutes
Explanation:
Given:
Time taken by Maria to print and laminate signs = 4 hours
Time taken by Josie to print and laminate signs = 2 hours
Solution:
Rate of work done by Maria =
 per hour
per hour
Rate of work done by Josie =
 per hour
per hour
Let them work for
 hours together.
hours together.
In
 hours work done by Maria =
hours work done by Maria =
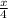
In
 hours work done by Josie =
hours work done by Josie =
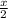
Total work done by both =
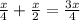
If they complete the work in
 hours, then we can write as:
hours, then we can write as:
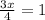
Solving for

Multiplying both sides by

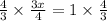
∴
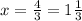 hours = 1 hour and 20 minutes [As
hours = 1 hour and 20 minutes [As
 of an hour =20 minutes.
of an hour =20 minutes.
So, Maria and Josie working together can complete the work in= 1 hour and 20 minutes