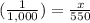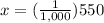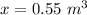Question

The scale factor of a model of a grain silo to the actual silo is 1 to 10. the volume of the actual silo is 550m3. what is the volume of the model

a.0.55 m ^3
b.2.75 m^3
c. 5.5 m ^3
d. 2.75 m^3

Answer 1

0.55 m^3

Explanation:

we have

substitute the values

Solve for x

Answer 2

Option a. 0.55 m ^3

Explanation:

we know that

If two figures are similar, then the ratio of its volume is equal to the scale factor elevated to the cubic

Let

z ----> the scale factor

x ----> the volume of the model of a grain silo in cubic meters

y ---> the volume of the actual silo in cubic meters

so

`z^(3) =(x)/(y)`

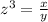
we have

`z=(1)/(10)`

`y=550\ m^3`

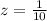
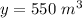
substitute the values

`((1)/(10))^(3) =(x)/(550)`

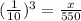
Solve for x

`((1)/(1,000)) =(x)/(550)`

`x=((1)/(1,000))550`

`x=0.55\ m^3`