Question

A rectangle has an area of 234 cm2 and a perimeter of 62 cm. What are its dimensions? It's length is ? Its width is? where length > width

Answer 1

Length of the rectangle is 18 cm

and Width is 13 cm.

Explanation:

Here, let us assume the length of the rectangle a cm

and the width of the rectangle = b cm

Now, Perimeter of the Rectangle = 2 (length + Width) = 62 cm

⇒ 2( a+ b ) = 62 cm

Area of the Rectangle = (length x Width) = 234 sq. cm

⇒ a x b = 234 sq. cm

Now, taking both the equations and simplifying for a and b , we get:

2( a+ b ) = 62 ⇒ (a + b) = 31 or, b = 31 -a

ab = 234

Substitute b = (31-a) in second equation

ab = 234 ⇒ a (31-a) = 234

or,
`31 a  - a^2 = 234\\\implies a^2 - 31a + 234 = 0\\a^2 - 13 a - 18 a + 234 = 0\\\implies (a-13)(a-18) =0\\\implies a  = 13, a = 18`

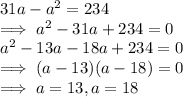
Now, if a = 13, b = 31 - 13 = 18 cm

and if a = 18, b = 31 - 18 = 13 cm

But, given Length > Width ⇒ a > b ⇒ a = 18 cm, b = 13 cm

Hence, the length of the rectangle is 18 cm and Width is 13 cm.