Answer:
Impossible
Explanation:
In 5x^2-4x+3=0, standard form, substitute these values in the quadratic formula:
a = 5; b = -4; c = 3
The quadratic formula is
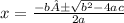
(ignore the weird capital A)
Substitute a b and c:
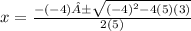
Simplify:
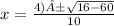
Because
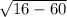 is the square root of a negative number, the answer would be imaginary.
is the square root of a negative number, the answer would be imaginary.
Therefore, there are not solutions to this equation.
A solution is the same as the roots or zeroes, where the graph would cross the x-axis when graphed.
The graph never meets the x-axis. It looks like this: