Question

A glass is half-full of water, with a layer of oil (n = 1.46) floating on top. A ray of light traveling downward through the oil is incident on the water at an angle of 73.7°. Take the refraction index of water to be 1.333. (a) Determine the critical angle for the oil-water interface. (b) Will the ray penetrate into the water?

Answer 1

a)
`\theta_c\approx65.92^(\circ)`

b) No, the ray will not penetrate into the water since 73.7° is greater than the critical angle.

Step-by-step explanation:

Given that:

refractive index of oil,
`n_1=1.46`

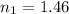
angle of incidence,
`\theta_1=73.7^(\circ)`

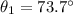
refractive index of water,
`n_2=1.333`

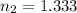
(a)

Snell's law states that when a ray of light travels from a denser medium to a rarer medium its speed increases and it bends away from the normal. Likewise, when a ray of light travels from a rarer medium to a denser medium its speed slows down and it bends towards the normal.

Mathematically:

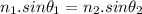`n_1.sin\theta_1=n_2.sin\theta_2`................................(1)

where the subscripts 1 & 2 denote for the incident ray and the refracted ray respectively.

Critical angle is that angle of incident of a ray of light through the optically denser medium on the two medium interface after which the refracted ray makes an angle of 90 degrees to the normal in the rarer medium.

• This is in accordance with the Snell's law that as we keep on increasing the the angle of incident on the optically denser side the angle of refraction keeps on increasing on the rarer side.

Now, using Snell's law eq. (1):

`1.46* sin\,\theta_c=1.333* sin\,90^(\circ)`

`sin\,\theta_c\approx 0.913`

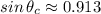
`\theta_c\approx65.92^(\circ)` is the critical angle.

(b)

Since we have critical angle 65.92 degrees, so any value of the angle of incidence greater than that will lead to the reflection of the light from the interface of the two mediums, this phenomenon is called the total internal reflection.