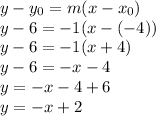Question

Write the equation of the line given points (-4,6) and (-8,10)

Answer 1

the equation of the line in slope-intercept form is:
`y=-x+2`

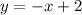
Explanation:

First start by finding the slope of the segment that joins those two points using the general formula for the slope of the segments between two points
`(x_1,y_1)` and
`(x_2,y_2)` on the plane:

`Slope=(y_2-y_1)/(x_2-x_1)`

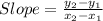
Then for our case, calling (-4, 6) =
`(x_1,y_1)` and (-8, 10) =
`(x_2,y_2)`, we have:

`Slope=(y_2-y_1)/(x_2-x_1)\\Slope=(10-6)/(-8-(-4))\\Slope=(4)/(-8+4)\\Slope=(4)/(-4)\\Slope= -1`

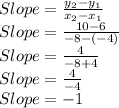
Now, knowing this, we can find the equation of the line by using the "point-slope" form of a line [of slope "m" and going through the point
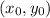`(x_0,y_0)` that tells us:

`y-y_0=m(x-x_0)`

We will be then using the found slope (-1) and for example one of the given points: (-4 , 6), thus:

`y-y_0=m(x-x_0)\\y-6=-1(x-(-4))\\y-6=-1(x+4)\\y-6=-x-4\\y=-x-4+6\\y=-x+2`