Question

An exit poll of 1000 randomly selected voters found that 515 favored measure A. a. Construct a 99% confidence interval for the support of measure A. b. Suppose measure A needs at least 50% support to pass, what are the null and alternative hypotheses if we were to test to see if measure A will pass? c. Compute the p-value of the above test.

Answer 1

Explanation:

Given that an exit poll of 1000 randomly selected voters found that 515 favored measure A.

Sample proportion p =
`(515)/(1000) =0.515`

`q=1-0.515 =0.485\\n =1000\\SE = \sqrt{(pq)/(n) } \\=0.158\\`

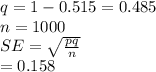
Margin of error 99% = 2.58*SE

=
`2.58*0.0158\\=0.0408`

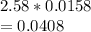
99% confidence interval =
`(0.515-0.0408, 0.515+0.0408)\\= (0.474, 0.556)`

------------------------

`H_0: p =0.5\\H_a: p >0.5\\`

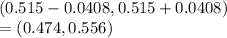
(Right tailed test)

STd error =
`\sqrt{(0.5*0.5)/(1000) } \\=0.0158`

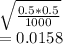
Test statistic Z = p diff/std error =
`(0.015)/(0.0158) \\\\=0.9487`

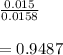
p value = 0.1714