Question

What is the energy of a photon that has a wavelength of 8.6x10^3nm?

Answer 1

The energy of the photon is
`2.311* 10^(-20)\ J`.

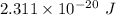Step-by-step explanation:

Given:

The wavelength of the photon is given as:

`\lambda =8.6* 10^3\ nm\\1\ nm = 10^(-9)\ m\\\therefore \lambda = 8.6* 10^(3)* 10^(-9)=8.6* 10^(-6)\ m`

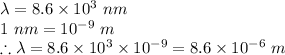
The energy of a photon in terms of its wavelength is given as:

`E_p=(hc)/(\lambda)\\Where,\ h\rightarrow \textrm{Planck's constant}=6.626* 10^(-34)\ Js\\c\rightarrow \textrm{velocity of light}=3* 10^8\ m/s`

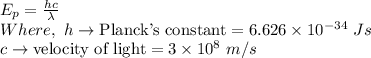
Plug in all the given values and calculate energy of the photon,
`E_p`. This gives,

`E_p=(6.626* 10^(-34) * 3* 10^8)/(8.6* 10^(-6))\\E_p=(19.878* 10^(-26))/(8.6* 10^(-6))\\E_p=2.311* 10^(-20)\ J`

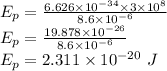
Therefore, the energy of the photon is
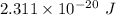`2.311* 10^(-20)\ J`.