Question

Find two consecutive integers such that the sum of their squares is 145.

Answer 1

Answer: 8 and 9 or -9 and -8

Explanation:

Let
`x` be the first of the two integers. Then, since the numbers are consecutive,
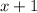`x+1` is the other integer. We then know that the sum of the squares of
`x` and
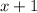`x+1` is equal to 145. So, now we have the equation

`x^2+(x+1)^2=145`

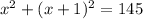
which can be expanded and simplified to

`2x^2+2x+1=145`

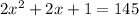
which then gives us the quadratic equation

`2x^2+2x-144=0`

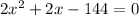
This can then be factored into

`2(x^2+x-72)=0`

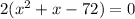
Which can be simplified further into

`2(x-8)(x+9)=0`

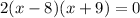
So either
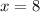`x=8` or
`x=-9`. This gives us two solutions: 8 and 9 or -9 and -8.

Hope this helps! CHEERS!