Question

You ride your bike to campus a distance of 6 miles and return home on the same route. Going to​ campus, you ride mostly downhill and average 5 miles per hour faster than on your return trip home. If the round trip takesnbsp two hours and nbsp10 minuteslong dashthat ​is, StartFraction 13 Over 6 EndFraction hourslong dashwhat is your average rate on the return​ trip?

Answer 1

Answer:v=4 mph

Explanation:

Given

Distance between school and home is 6 miles

let v be the speed during return trip in miles/hr

total time taken
`=2 hr 10 min \approx (13)/(6) hr`

During arrival
`t_1=(6)/(v+5)`

During Return
`t_2=(6)/(v)`

Total time
`t_1+t_2=(13)/(6)`

`(6)/(v+5)+(6)/(v)=(13)/(6)`

`6((1)/(v+5)+(1)/(v))=(13)/(6)`

`6\cdot (2v+5)/(v(v+5))=(13)/(6)`

`72v+180=13v^2+65v`

`13v^2-7v-180=0`

`v=(7\pm √(7^2+4* 13* 180))/(2* 13)`

`v=4 mph`

Thus velocity during return trip
`v=4 mph`

Answer 2

1.98 miles per hour.

Explanation:

Let x miles per hour be the average rate on the return​ trip,

∵ The speed on round trip is 5 miles per hour faster than on return trip,

So, the speed in round trip = (x+5) miles per hour,

Now, distance in one sided trip = 6 miles,

Since,

`Speed = (Distance)/(Time)\implies Time = (Distance)/(Speed)`

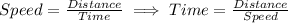
According to the question,

Time taken in return trip - Time taken in round trip =
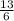`(13)/(6)` hours,

`\implies (6)/(x)-(6)/(x+5)=(13)/(6)`

`(6x+30-6x)/(x(x+5))=(13)/(6)`

`(30)/(x^2 + 5x)=(13)/(6)`

`180 = 13x^2 + 65x`

`13x^2 + 65x - 180 = 0`

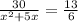
By quadratic formula,

`x=(-65\pm √(65^2 - 4* 13* -180))/(26)`

`x=(-65\pm √(4225 + 9360))/(26)`

`x=(-65\pm √(13585))/(26)`

`x\approx 1.98\text{ or }x=-6.98`

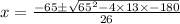
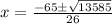
∵ speed can not be negative,

Hence, average rate on the return​ trip would be 1.98 miles per hour.