Answer:
fem = - 4.50 10²² V
Step-by-step explanation:
For the solution of this problem we must use the equation of the induced electromotive force or Faraday's law
E = - d Φ
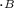 / dt = d (BA cos θ) dt
/ dt = d (BA cos θ) dt
In this case they tell us that the magnetic field is perpendicular to the plane of the loop, as the normal to the surface of the loop is in the direction of the radius, the angle between the field and this normal is zero, so cos 0º = 1. The area of the loop is constant, with this the equation is
E = - A dB / dt (1)
To find field B, we have the relationships of electromagnetic waves
E = c B
The intensity or poynting vector for the wave is described by the equation
S = I = 1 / μ₀ E x B = 1 /μ₀ E B
We replace
I = 1 /μ₀ (cB) B = c /μ₀ B²
This is the instantaneous intensity.
B = √ (μ₀ I /c)
We substitute in equation 1
E = - A μ₀/c d I / dt
With the maximum value we are asked to change it derived from variations
E = -A c/μ₀ ΔI / Δt
It remains to find the time of the variation. Let's use the equation
c = λ f = λ / T
T = λ / c
T = 6.20 / 3 10⁸
T = 2.06 10⁻⁸ s
We already have all the values to calculate the fem
fem = - π r² c/μ₀ ΔI/Δt
fem = - (π 0.078²) (3 10⁸/(4π 10⁻⁷) (2.03 10² -0) / (2.06 10⁻⁸ - 0)
fem = - 4.50 10²² V