Question

A liquid of density 1288 kg/m3 flows with speed 2.88m/s into a pipe of diameter 0.24 m. The diameter of the pipe decreases to 0.05 m at its exit end. The exit end of the pipe is 3.34 m lower than the entrance of the pipe, and the pressure at the exit of the pipe is 1.4 atm.

a) What is the velocity v2 of the liquid flowing out of the exit end of the pipe? Assume the viscosity of the fluid is negligible and the fluid is incompressible. The acceleration of gravity is 9.8 m/s2 and Patm = 1.013

Answer 1

66.35m/s

Step-by-step explanation:

Para resolver el ejercicio es necesario la aplicación de las ecuaciones de continuidad, que expresan que

`A_1V_1 =A_2 V_2`

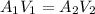
From our given data we can lower than:

`R_i = (0.24)/(2) = 0.12m`

`R_f = (0.05)/(2) = 0.025m`

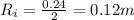
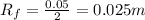
So using the continuity equation we have

`A_1V_1 =A_2 V_2`

`V_2 = (A_1V_1)/(A_2)`

`V_2 = ((\pi(0.12^2))(2.88))/((\pi (0.25)^2))`

`V_2 = 66.35m/s`

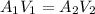
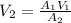
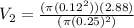
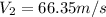
Therefore the velocity at the exit end is 66.35m/s