Question

he American Heart Association is about to conduct an anti-smoking campaign and wants to know the fraction of Americans over 45 who smoke. Step 2 of 2: Suppose a sample of 830 Americans over 45 is drawn. Of these people, 631 don't smoke. Using the data, construct the 85% confidence interval for the population proportion of Americans over 45 who smoke. Round your answers to three decimal places.

Answer 1

The 85% confidence interval is (0.2187, 0.2613).

Explanation:

We have a large sample of size n = 830 Americans over 45. We have observed that 631 people don't smoke. Let p be the population proportion of Americans over 45 who smoke. An point estimate of p is
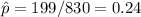`\hat{p} = 199/830 = 0.24` and an estimate of the standard deviation of
`\hat{p}` is
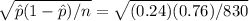`\sqrt{\hat{p}(1-\hat{p})/n} = √((0.24)(0.76)/830)` = 0.0148. Therefore, because we have a large sample, the 85% confidence interval for the population proportion is given by
`\hat{p}\pm z_(\alpha/2)\sqrt{\hat{p}(1-\hat{p})/n} = 0.24\pm z_(0.15/2)0.0148 = 0.24\pm z_(0.075)0.0148` where
`z_(0.075)` is the 7.5th quantile of the standard normal distribution, i.e., -1.4395. Therefore the 85% confidence interval is
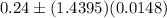`0.24\pm (1.4395)(0.0148)` or equivalently (0.2187, 0.2613).