Answer:
The sum of first seventeen terms is - 510
Explanation:
Given as :
The 4th term of an A.P =
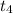 = - 15
= - 15
The 9th term of an A.P =
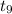 = - 30
= - 30
For an arithmetic progression
The nth term is given as
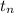 = a + ( n - 1)×d
= a + ( n - 1)×d
Where a is the first term and d is the common difference between numbers
So, For 4th term
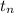 = a + ( n - 1)×d
= a + ( n - 1)×d
Or,
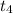 = a + ( n - 1)×d
= a + ( n - 1)×d
- 15 = a + ( 4 - 1)×d
Or, - 15 = a + 3 d .........1
So, For 9th term
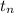 = a + ( n - 1)×d
= a + ( n - 1)×d
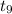 = a + ( n - 1)×d
= a + ( n - 1)×d
- 30 = a + ( 9 - 1)×d
Or, - 30 = a + 8 d .........2
Solve eq 1 and 2
( a + 8 d ) - ( a + 3 d ) = - 30 - ( - 15)
or, ( a - a ) + ( 8 d - 3 d ) = - 30 + 15
or, 0 + 5 d = - 15
∴ d = -
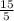 = - 3
= - 3
Now, put the value of d in eq 1
I.e - 15 = a + 3 × ( - 3)
Or. - 15 = a - 9
∴ a = -15 + 9 = - 6
Now The sum of nth term is written as :
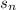 =
=
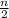 × [ 2 × a + ( n - 1 )×d ]
× [ 2 × a + ( n - 1 )×d ]
Where n is the nth term
a is the first term
d is the common difference
So For n = 17th term
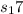 =
=
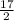 × [ 2 × ( - 6) + ( 17 - 1 )×( - 3) ]
× [ 2 × ( - 6) + ( 17 - 1 )×( - 3) ]
Or,
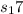 =
=
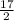 × [ - 12 - 48 ]
× [ - 12 - 48 ]
Or,
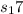 =
=
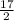 × ( - 60 )
× ( - 60 )
Or,
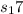 = 17 × ( - 30)
= 17 × ( - 30)
∴
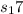 = - 510
= - 510
Hence The sum of first seventeen terms is - 510 Answer