Question

Peter and Paul agree to meet at a restaurant at noon. Peter arrives at a time normally distributed with mean 12:00 noon, and standard deviation 5 minutes. Paul arrives at a time normally distributed with mean 12:02 P.M., and standard deviation 3 minutes. Assuming the two arrival times are independent, find the chance that

(a) Peter arrives before Paul;
(b) both men arrive within 3 minutes of noon;
(c) the two men arrive within 3 minutes of each other.

Answer 1

0.5137,0.3082,0.3955

Explanation:

Let X be the arriving time of Peter and Y of Paul.

X is N(12,5) Y Is N(12.02, 3)

Hence X-Y is normal with mean
`=12-12.02 =-0.02`

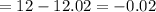
Variance =
`5^2+3^2 =34`

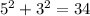
Std dev = 5.831

X-Y is N(-0.02, 5.831)

a) Prob Peter arrives before Paul;

=
`P((X-Y)\leq 0)=P(Z\leq (0.2)/(5.831) ) \\=0.5137`

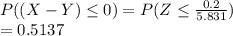
b) both men arrive within 3 minutes of noon;

=
`P(|x-12|<3) *P(|Y-12.02|<3\\= P(|Z|<0.6)*P(|z|<1)\\= 0.4514*0.6826\\=0.3082`

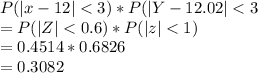
c) both men arrive within 3 minutes of noon;

=
`P(|x-y|<3)= P(|z|<(3.02)/(5.831) \\=P(|z|<0.52)\\=0.3955`