Question

Can someone please help me!

Answer 1

Problem 5:

Answer a) = 16 m

JH = 14 m

GJ = 19 m

answer d) =
`105^o`

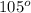
< G =
`34^o`

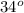
< J =
`41^o`

Problem 6:

x = 13

Explanation:

Problem 5: Notice from the drawing that the following vertices are congruent:

G same as D

J same as E

and

H same as the remaining vertex

Therefore DF = GH = 16 m

JH = EF = 14 m

GJ = DE = 19 m

and for the angles:

< H =
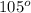`105^o` and equal to its equivalent in the other triangle.

< G = < D =
`34^o`

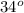
and the remaining angle (<J) can be obtained by using that the addition of the three angles in a triangle should equal
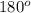`180^o`. That is: <J + <H + <G =
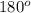`180^o`, therefore <J +
`34^o` +
`105^o` =
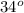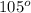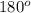`180^o`, then:

<J =
`180^o` -
`34^o` -
`105^o` =
`41^o`

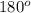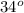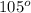Problem 6: An equilateral triangle has all equal sides, and therefore all equal angles opposing the sides. Therefore all three angles must be equal, and add to
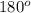`180^o`, Then each angle should be equal to
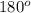`180^o`/3 =
`60^o`.

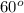So in order to find "x" we need to find the unknown that makes the following equation true:

8 x - 44 = 60

8 x = 60 + 44

8 x = 104

x = 104/8

x = 13