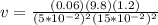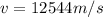Our values given are:
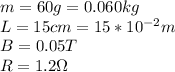
For the second Newton Law we have,
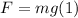
And for the Faradays equation we have that
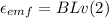
Where,
B= Magnetic field
L = Lenght
v = velocity
However for the Ohm's Law we have that
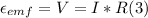
V = Voltage
I = Current
R = Resistance
Equating equation (2) and (3)
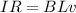
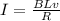
The magnetic force on a charged particle depends on the relative orientation of the particle's velocity and the magnetic field. And it is defined as,
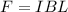
Replacing the previous value of the current,
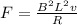
And replacing the value of the force given by Newton we have,
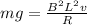
Re-arrange to find the velocity,
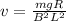
We can now replace the values of this problem,