Question

Which of the following shows that polynomials are closed under subtraction when two polynomials, (4x2 − 8x − 7) − (3x2 − 5x + 16), are subtracted?

x2 − 3x − 23; will be a polynomial
x2 − 3x − 23; may or may not be a polynomial
x2 − 13x + 9; will be a polynomial
x2 − 13x + 9; may or may not be a polynomial

Answer 1

x^2 − 3x − 23; will be a polynomial

Explanation:

(Took test)

Answer 2

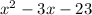`x^(2) -3x-23`; will be a polynomial

Explanation:

Given:

Two polynomials
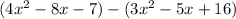`(4x^(2) - 8x -7)- (3x^(2)-5x + 16)`has to be subtracted

`(4x^(2) - 8x -7)- (3x^(2)-5x + 16)\\4x^(2) - 8x -7- 3x^(2)+5x -16\\4x^(2) - 3x^(2)- 8x+5x -16 -7\\x^(2) - 3x -23`

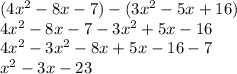
By Definition of polynomial which states:

"A polynomial is an algebraic expression with a finite number of terms and are termed in the form "axn" where "a" is a real number, "x" means to multiply, and "n" is a non-negative integer."

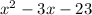`x^(2) -3x-23`; will be a polynomial