Question

A 1300 kg weather rocket accelerates upward at 10m/s2. It explodes 1.5 s after liftoff and breaks into two fragments, one twice as massive as the other. Photos reveal that the lighter fragment traveled straight up and reached a maximum height of 500 m . Part A What was the speed of the heavier fragment just after the explosion?

Answer 1

To solve this problem it is necessary to apply the conservation equations of the Momentum. The equation that represents such momentum conservation is given by,

Final momentum = Initial momentum

`m_1v_2+m_2v_2 = (m_1+m_2)v`

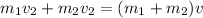
Where,

`m_1`=mass light

`m_2` = mass heavy

`v_1`= velocity of mass light

`v_2` = velocity of mass heavy

`v_f` = final velocity

One of the masses is heavier than the other previously detached so we will assume that mass is 1/3 of the total, and the heavy mass is 2/3 of the total.

We start finding the initial velocity, then

`V=a*t`

`V=10m/s^2*2s = 20 m/s`

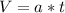
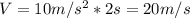
The distance traveled is then calculated by the kinematic equations of motion,

`X = V_0 t+(1)/(2)at^2`

`X=0+(1)/(2)*10*4`

`X=20m`

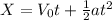
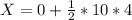
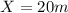
The speed of the lighter piece is given also for the kinematic equation of movement,

`V_f = V_i-2ax`

`0 = V_i - 2*9.81*(500-20)`

`v_i=9417.6`

`v_i=97.04 m/s`

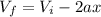
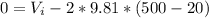
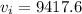
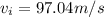
Replacing at the conservation of momentum equation we have,

`m_1v_2+m_2v_2 = (m_1+m_2)v`

`(1300*(1)/(3))*97.04 + (1300*(2)/(3))*V_2= 1300*20`

`26000 = 42050.66 + 866.66V_2`

`V_2= -18.52 m/s`

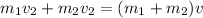
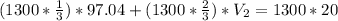
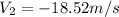
Therefore the speed of the heavier fragment just after the explosion is 18.52m/s against the direction of movement.