Question

g Two out of thirteen members of a school board feel that all high school students should be required to take a course in coding. A pollster selects four members of the board at random and asks them for their opinion on requiring a coding course. What is the probability that at least one of the members polled favors requiring the​ course?

Answer 1

There is a probability of 48.73% that at least one of the members polled favors requiring the​ course

Explanation:

For each member asked, there are only two possible outcomes. Either they feel that all high school students should be required to take a course in coding, of they feel they shouldn't. This means that we can solve this problem using the binomial probability distribution.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

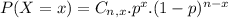
In which
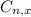`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

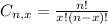
And p is the probability of X happening.

In this problem we have that:

Four members are selected, so
`n = 4`.

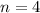Two out of thirteen members of a school board feel that all high school students should be required to take a course in coding. This means that
`p = (2)/(13) = 0.1538`.

What is the probability that at least one of the members polled favors requiring the​ course?

Either none of them favor requiring the course, or at least one do. The sum of the probabilities of these events is decimal 1. So:

`P(X = 0) + P(X > 0) = 1`

`P(X > 0) = 1 - P(X = 0)`

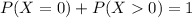
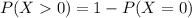
In which

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(4,0).(0.1538)^(0).(0.8462)^(4) = 0.5127`

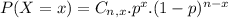
So

`P(X > 0) = 1 - P(X = 0) = 1 - 0.5127 = 0.4873`

There is a probability of 48.73% that at least one of the members polled favors requiring the​ course