(a) A box plot shows the distribution of the data and any outliers. The new diet has a higher mean and a larger range of values than the old diet.
(b) A two-sample t-test is used to test the hypotheses. The t-statistic is 5.93, which is greater than 2.571. The null hypothesis is rejected at α=0.05.
The scientist randomly assigns 8 cows to the old diet and 5 cows to the new diet. After two weeks, the scientist milks each cow and records the amount of milk produced in pounds.
Old Diet: 43, 51, 44, 47, 38, 46, 40, 35
New Diet: 47, 75, 85, 100, 58
Let
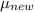 and
and
 be the population mean milk productions for the new and old diets, respectively. The scientist wishes to test
be the population mean milk productions for the new and old diets, respectively. The scientist wishes to test
![[H_(0): \mu_(new) - \mu_(old) = 0]](https://img.qammunity.org/2020/formulas/mathematics/college/klebm8b68b0qu3b6s2hkm2d3rm267c6zwy.png)
VS.
![[H_(1): \mu_(new) - \mu_(old) \\eq 0]](https://img.qammunity.org/2020/formulas/mathematics/college/wxghspegek2rpbn72mr80lg255pojc5guw.png)
using α=0.05.
(a)
A box plot is a good way to graph the data because it shows the distribution of the data and any outliers. The box plot shows that the new diet has a higher mean and a larger range of values than the old diet.
(b) Choose a test appropriate for the hypotheses and justify your choice based on your answer to part (a). Then perform the test by computing a p-value, and making a reject or not reject decision. Do this without R and show your work. (Also do it with R. if you wish, to check your work). Finally, state your conclusion in the context of the problem.
Since the box plot shows that the new diet has a higher mean than the old diet, we can use a two-sample t-test to test the hypotheses. The formula for the two-sample t-statistic is
![[\frac{\bar{x}{new} - \bar{x}{old}}{\sqrt{(\sigma^2_(new) + \sigma^2_(old))/(2)}}]](https://img.qammunity.org/2020/formulas/mathematics/college/xl08ldxwminqr0p42hfyry2bifzuabjvrw.png)
where
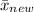 and
and
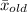 are the sample means for the new and old diets, respectively, and
are the sample means for the new and old diets, respectively, and
 and
and
 are the sample variance for the new and old diets, respectively.
are the sample variance for the new and old diets, respectively.
The sample means are
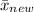 =65.2 pounds and
=65.2 pounds and
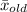 =45.2 pounds, the sample variances are
=45.2 pounds, the sample variances are
 = 172.24 pounds and
= 172.24 pounds and
 =82.24 pounds. Substituting these values into the formula for the t-statistic, we get
=82.24 pounds. Substituting these values into the formula for the t-statistic, we get
![[\frac{65.2 - 45.2}{\sqrt{(172.24 + 82.24)/(2)}} = 5.93.]](https://img.qammunity.org/2020/formulas/mathematics/college/tleqjrim2wd7mp9r3taalg943yt08b6s85.png)
The t-statistic is greater than 2.571, so we reject the null hypothesis at α=0.05.