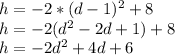Question

The height of a fountain’s water stream can be modeled by a quadratic function. Suppose the water from a jet reaches a maximum height of 8 feet at a distance 1 foot away from the jet. If the water lands 3 feet away from the jet, find a quadratic function that models the height h(d) of the water at any given distance d feet from the jet.

Answer 1

h(d)= -2d^2 +4d +6

Explanation:

Vertex (1,8)

Landing Point (3,0)

Applying the vertex formula, a quadratic equation can be described by its vertex v(x,y) as follows:

`h=a*(d-x)^2 +y`

Since the vertex in this situation is at v (1,8):

`h=a*(d-1)^2 +8`

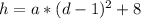
To solve for 'a', apply the other given point (landing point) into the equation:

`0=a*(3-1)^2 +8\\4a= - 8 \\a=-2`

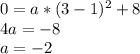
Expanding the equation yields:

`h=-2*(d-1)^2 +8\\h=-2(d^2 -2d +1) +8\\h= -2d^2 +4d +6\\`