Question

Many medical professionals believe that eating too much red meat increases the risk of heart disease and cancer (WebMD website, March 12, 2014).

Suppose you would like to conduct a survey to determine the yearly consumption of beef by a typical American and want to use 3 pounds as the desired margin of error for a 99% confidence interval of the population mean amount of beef consumed annually.
Use 25 pounds as a planning value for the population standard deviation.

How large a sample should be taken?

Answer 1

Answer: 461

Explanation:

Formula to find the sample size is given by :-

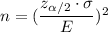`n=((z_(\alpha/2)\cdot \sigma)/(E))^2` , where n is the sample size ,
`\sigma` is the population standard deviation and
`z_{\alpha/2` is the two tailed test value of z for significance level (
`\alpha`).

Given :
`\sigma=25\text{ pounds}`

Margin of error : 3 pounds

Confidence level = 99%

Significance level :
`\alpha=1-0.99=0.01`

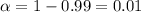
Critical value :
`z_(\alpha/2)=z_(0.005)=2.576`

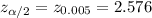
Then, the required minimum sample size would be :-

`n=(((2.576)\cdot (25))/(3))^2\approx460.817777778\approx461`

Hence, the required minimum sample size = 461