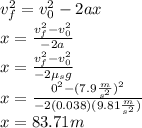Question

A girl coasts down a hill on a sled, reaching level ground at the bottom with a speed of 7.9 m/s. The coefficient of kinetic friction between the sled’s runners and the hard, icy snow is 0.038, and the girl and sled together weigh 750 N. The acceleration of gravity is 9.81 m/s 2 . How far does the sled travel on the levelground before coming to a rest? Answer in units of m.

Answer 1

`x=83.71m`

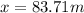
Step-by-step explanation:

The frictional force is given by:

`F_f=\mu_s N(1)`

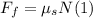
According to Newton's second law:

`\sum F_y:N=W(2)\\\sum F_x:F_f=ma(3)`

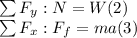
Replacing (2) and (3) in (1):

`ma=\mu_s W(4)`

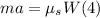
To find the mass of the girl on the sled, we divide their weigh into the acceleration of gravity:

`W=mg\\m=(W)/(g)(5)\\`

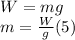
Replacing (5) in (4). Solving for a:

`(W)/(g)a=\mu_s W\\a=\mu_s g`

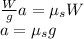
Finally, using this kinematic equation, we calculate the distance traveled before coming to a rest (
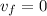`v_f=0`):

`v_f^2=v_0^2-2ax\\x=(v_f^2-v_0^2)/(-2a)\\x=(v_f^2-v_0^2)/(-2\mu_s g)\\x=(0^2-(7.9(m)/(s^2))^2)/(-2(0.038)(9.81(m)/(s^2)))\\x=83.71m`