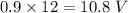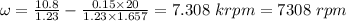Question

A motor with KT = 1.657 in-oz/A, Ke = 1.23 V/krpm and terminal resistance R = 20Ω is driven at 12 V. Assume VPWM = duty cycle*Vdd. a) How fast will the motor spin under a constant 0.15 in-oz load if it is driven by PWM with a 25% duty cycle and a frequency well above the motor’s time constants? b) What is the speed if the duty cycle is increased to 90%?

Answer 1

(a) 9607 rpm

(b) 7308 rpm

Solution:

As per the question:

`K_(T) = 1.657\ in-oz/A`

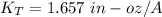
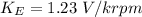
`K_(E) = 1.23\ V/ krpm`

R =
`20\Omega`

`V_(dd) = 12\V`

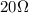
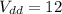
From the question:

V =
`D* V_(dd)`

`V = 12* 0.25 = 3 V`

`Constant\ Load, T = 0.15\ in-oz`

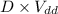
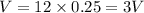
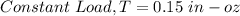
Duty cycle, D = 25% = 0.25

(a) Angular speed of the motor,
`\omega` can be calculated as:

EMF of the motor is given by:

E = V - IR

where

Also,

`E = k_(E)\omega`

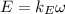
`\omega = (E)/(K_(E)) = (V - IR)/(K_(E))` (1)

Now,

Torque, T =
`K_(T)I`

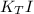
Thus

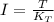`I = (T)/(K_(T))` (2)

From eqn (1) and (2)

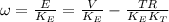
`\omega = (E)/(K_(E)) = (V)/(K_(E)) - (TR)/(K_(E)K_(T))`

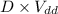
V =
`D* V_(dd)`

V =
`0.25* 12 = 3\ V`

`\omega = (3)/(1.23) - (0.15* 20)/(1.23* 1.657) = 0.967\ krpm = 967\rpm`

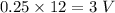
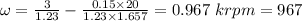
(b) Speed of the motor when D = 90% = 0.9

V =
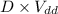
`D* V_(dd)`

V =
`0.9* 12 = 10.8\ V`

`\omega =  (V)/(K_(E)) - (TR)/(K_(E)K_(T))`

`\omega = (10.8)/(1.23) - (0.15* 20)/(1.23* 1.657) = 7.308\ krpm = 7308\ rpm`