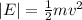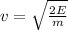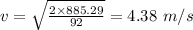Answer:
The speed of the rock is 4.38 m/s.
Solution:
As per the question:
Mass of the gold space rock, m = 92 kg
Force exerted by the tractor beam,
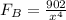
Now,
Suppose that the spaceship started to apply force when it reaches a distance of 7 m until it gets close to 2m distance, in this case the energy, E can be given as:
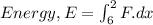
![E = 902* [- (1)/(x^(3))]_(6)^(2) = 885.29\ J](https://img.qammunity.org/2020/formulas/physics/college/wkbsete5w681usre62rgnfd0rfsuahdwue.png)
Now,
To calculate the speed, the gain in Kinetic energy of the rock is given by: