Question

A heat pump is used to maintain a house at 22°C by extracting heat from the outside air on a day when the outside air temperature is 2°C. The house is estimated to lose heat at a rate of 110,000 kJ/h, and the heat pump consumes 5 kW of electrical power when running. Is this heat pump powerful enough to do the job?

Answer 1

The heat pump is not powerful enough; it can supply only 20 kW of heat output, while the house loses heat at a rate of 30.56 kW.

Step-by-step explanation:

To determine if the heat pump is powerful enough to maintain a house at 22°C, we must compare the heat loss with the heat supplied by the pump. A rate of heat loss at 110,000 kJ/h translates to 110,000/3600 kJ/s, which is about 30.56 kW. Since the heat pump consumes 5 kW of electrical power, we need to know the Coefficient of Performance (COP) to calculate the heat it can provide.

The COP depends on the temperatures of the cold and hot reservoirs, but a typical real-world COP value ranges from 2 to 4. Assuming the best scenario of a COP of 4, the heat provided by the pump would be 4 times the electrical power input. Therefore, 5 kW × 4 equals 20 kW of heat output. Comparing the pump's heat output (20 kW) with the house's heat loss (30.56 kW), we can see that the heat pump is not powerful enough to offset the heat loss. The house requires a pump that can supply at least 30.56 kW of heat to maintain the temperature at 22°C when the outside temperature is 2°C.

Answer 2

It is enough

Step-by-step explanation:

To develop the problem it is necessary to take into account the concepts related to the coefficient of performance of a pump.

The two ways in which the performance coefficient can be expressed are given by:

`COP_p = (T_H)/(T_H-T_L)`

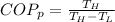
Where,

`T_H =`High Temperature

`T_L =` Low Temperature

And the other way is,

`COP_p = \frac{\dot{Q}}{W}`

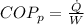
Where
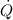`\dot{Q}` is heat rate and W the power consumed.

We have all our terms in Celsius, so we calculate the temperature in Kelvin

`T_H = 22+273 = 295K`

`T_L = 2+273 = 275k`

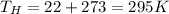
The rate at which heat is lost is:

`\dot{Q} = 110000kJ/h`

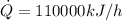
The power consumed by the heat pump is

`\dot{W} = 5kW`

And the coefficient of performance is

`COP_p = (T_H)/(T_H-T_L)`

`COP_p = (295)/(295-275)`

`COP_p = 14.75`

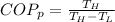
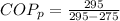
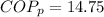
With this value we can calculate the Power required,

`COP_p = \frac{\dot{Q}}{W}`

`14.75 = (110000)/(W)`

`W = (110000)/(3600*14.75)`

`W = 2.07kW`

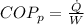
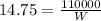
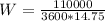
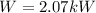
The power consumed is consumed is 5kW which is more than 2.07kW so this heat pump powerful enough.