Question

A railroad hopper car filled with sand is rolling with an initial speed of 15.0 m/s on straight horizontal tracks. Ignore frictional forces on the railroad car. The total mass of the car plus sand is 89000 kg. The hopper door is not fully closed, so sand leaks out the bottom. After 20 min, 17000 kg of sand leaked out. What then is the speed of the railroad car?

Answer 1

v=18.54167 m/s

Step-by-step explanation:

the law of linear momentum conservation says that when the resultant force in an object is null, the linear momentum is constant over time, so in accordance the paragrapfh the railroad car is moving and the forces acting on it is the weight and the normal force, so we can say that the resultant force on the railroad car are equal to zero

So, the linear momentum can be written

`V_(1)*m_(1)=  V_(2)*m_(2)`

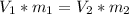
V_{1}= 15m/s

m1= 89000 kg

To the m2 we subtract the weight of sand that leak out

m2= 89000 kg - 17000 kg =72 000 kg

V_{2}=
`(89000*15)/(72000)`

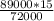
V_{2}= 18.54167 m/s