Answer:
See answer
Step-by-step explanation:
Given quantities:
![\eta = 0.05\\ W=90[W]\\r=0.0285[m]](https://img.qammunity.org/2020/formulas/physics/college/2pks7jjacbaebeblsr0761ism12qloz92y.png)
where
 is the efficiency of the lightbulb (visible light is 5% of the total power),
is the efficiency of the lightbulb (visible light is 5% of the total power),
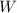 is the total power of the lightbulb, r is the radius of the lightbulb in meters.
is the total power of the lightbulb, r is the radius of the lightbulb in meters.
Intensity is power divided by area:
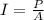
a) Now the effective power is
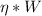 , therefore:
, therefore:
![I =(\eta*W)/(\pi r^2)=(0.05*90)/(4\pi (0.0285)^2)=440.87[W/m^2]](https://img.qammunity.org/2020/formulas/physics/college/4k8pil1xu01iac45m6ec6tvqfddgk0e8e2.png)
b) Now the intensity is the average poynting vector is related to the magnitudes of the maximum electric field and magnetic field amplitudes, following:
![S_(average)= (EB)/(2\mu_(0))[W/m]](https://img.qammunity.org/2020/formulas/physics/college/pf7ri5rpkm5r77px48650nbuqpcsgovzi7.png)
now
 and
and
 are related:
are related:
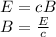 and
and

replace in

![S_(average)=I= (c \epsilon_(0)E^2)/(2)[W/m]](https://img.qammunity.org/2020/formulas/physics/college/q5fbqqw7als4ylbgwmpyzof6l99yw8iuec.png)
we replace the values and we get:
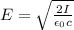
![E = \sqrt{(2(440.8))/(8.85*10^(-12)3*10^8)}=576.24[V/m]](https://img.qammunity.org/2020/formulas/physics/college/5my460l7c7p3chzb81voxz5j6fkhvfd9so.png)
therefore
![B=(E)/(c)=(576.24)/(3*10^(8))=1.92*10^(-6)[T]](https://img.qammunity.org/2020/formulas/physics/college/2hlb4h5ovsbgdxdkqenrnwxicyft9dj0ym.png)