Answers:
a) 19.937 s
b) 299 m
Step-by-step explanation:
a) Firstly, we have to establish the equations of motion for both the speeder and the police officer:
For the speeder, its velocity
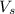 is:
is:
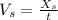
So, its position
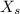 is:
is:
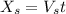 (1)
(1)
Where
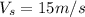 and
and
 the time
the time
For the police officer, its position
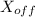 is:
is:
 (2) Because the officer began to drive after 9 seconds
(2) Because the officer began to drive after 9 seconds
Where
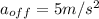
Now, when the position of both the officer and the speeder is the same (
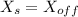 ) is when the officer catches the speeder, hence:
) is when the officer catches the speeder, hence:
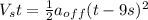 (3)
(3)
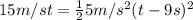 (4)
(4)
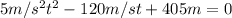 (5)
(5)
Applying common factor 5:
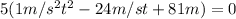 (6)
(6)
This can be rewritten as:
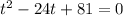 (7)
(7)
Solving for
 we have two results:
we have two results:

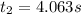
We choose
 , remembering the police officer began to drive
, remembering the police officer began to drive
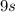 after the other car passed by its side. So, the time is 19.937 s.
after the other car passed by its side. So, the time is 19.937 s.
b) Now, if we want to know the distane the police officer drove before catching the speeder, we have to input the calculated time in the officer's equation (2):
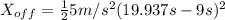 (8)
(8)
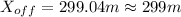 (9)
(9)
If we want to prove this is the same distance the other car drove, we have to input also this time (1):
 (10)
(10)
 (11)
(11)