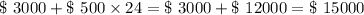Answer:
A. Total Money Contributed after n months =
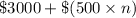
B. Total Money Contributed after 24 months =
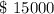
Explanation:
Given:
Initial contribution =
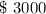
each month contribution =
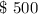
After 1 month contributed =
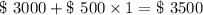
Solving for Part A
let n be the number of months
∴ Total Contribution after n months = Initial contribution + (each month contribution
 Number of months =
Number of months =
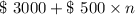
Solving for Part A
Now n= 24 months
∴ Total Contribution after 24 months =