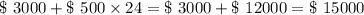Question

fabiana decides to save the money she is earning from her after school job for college. she makes an initial contribution of 3000$ and each month deposits an additional $500. After one month she will have contributed $3500.A. white an equation for the nth term of the sequence B. how much money will she have contribute after 24 month

Answer 1

A. Total Money Contributed after n months =
`\$ 3000 + \$ (500* n)`

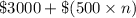
B. Total Money Contributed after 24 months =
`\$ \ 15000`

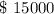
Explanation:

Given:

Initial contribution =
`\$\ 3000`

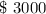
each month contribution =
`\$\ 500`

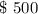
After 1 month contributed =
`\$\ 3000 + \$\ 500 * 1= \$ \ 3500`

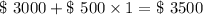
Solving for Part A

let n be the number of months

∴ Total Contribution after n months = Initial contribution + (each month contribution
`*` Number of months =
`\$\ 3000 + \$\ 500 * n`

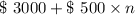
Solving for Part A

Now n= 24 months

∴ Total Contribution after 24 months =
`\$\ 3000 + \$\ 500 * 24 = \$\ 3000 + \$\ 12000= \$\ 15000`