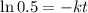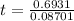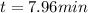Question

The temperature of a pan of hot water varies according to Newton's Law of Cooling: dT dt equals negative k times the quantity T minus A , where T is the water temperature, A is the room temperature, and k is a positive constant. If the water cools from 90°C to 85°C in 1 minute at a room temperature of 30°C, how long (to the nearest minute) will it take the water to cool to 60°C?

Answer 1

Answer:7.96 min

Step-by-step explanation:

Given

time taken by water to cool from
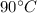`90^(\circ)C` to
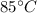`85^(\circ)C` is 1 min

Ambient Temperature
`T_(\infty )=30^(\circ)C`

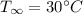
According to Newtons law of cooling

`(T-T_(\infty ))/(T_i-T_(\infty ))=e^(-kt)`

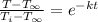
where T=Final Temperature

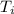`T_i`=Initial Temperature

k=time constant

t=time

`(85-30)/(90-30)=e^2{-k\cdot 1}`

`(11)/(12)=e^(-k)`

`k=0.08701`

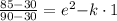
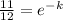
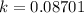
Time taken to cool to
`60^(\circ)C`

`(60-30)/(90-30)=e^(-kt)`

`(1)/(2)=e^(-kt)`

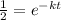
taking Log

`\ln 0.5=-kt`

`t=(0.6931)/(0.08701)`

`t=7.96 min`