Question

A native Australian named Anatjari wishes to cross a desert carrying only a sin- gle water bottle. He has a map that marks all the watering holes along the way. Assuming he can walk k miles on one bottle of water, design an efficient algo- rithm for determining where Anatjari should refill his bottle in order to make as few stops as possible. Argue why your algorithm is correct.

Answer 1

Consider that
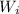`W_(i)` be the
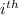`i^(th)` water hole

let D be the distance vector for all distances between watering holes.D[i] represents

the distance between
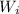`W_(i)` and
`W_(i+1)`

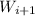
K be the distance he can walk with one bottle water.

Let's start with the first water hole.

Stops represents the set of stops={}

i=1

while(Wi Exists)

Distance=D[i]

while(Distance<k)

Distance=Distance+D[i+1]

i=i+1

Put Wi in Stops if Wi+1 exists

return set of Stops

the above algorithm checks if sum of consecutive distances are less than the value of k.

if the sum of distance exceeds value of k.

we put the current water hole to the set of stops.

Step-by-step explanation:

Proof

let's say distance vector D= {5, 15, 20, 15}

water holes W={W1, W2 , W3 ,W4 ,W5 }

k=25 be the max distance with single bottle.

after the algorithm

step1: distance=5 < 25 i=1

step2: distance=5+15 <25 i=2

step3: distance=20+15 >25 i=3 put W3 in Stops because W4 exists

step4: distance=D[3]=20<25 i=4

step5: distance=20+15>25 i=5 don't put W6 does not exists