Question

Michmoo Computer Company sells computers and computer parts by mail. The company assures its customers that products are mailed as soon as possible after an order is placed. A random sample of 62 recent orders showed that the mean time taken to mail products for these orders was 65 hours. Assume that the population standard deviation is 18 hours. Estimate with 93% confidence the mean time taken to mail products for all orders received at the office of this company.

Answer 1

Answer: (60.858, 69.142)

Explanation:

The formula to find the confidence interval for mean :

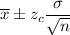`\overline{x}\pm z_c(\sigma)/(√(n))` , where
`\overline{x}` is the sample mean ,
`\sigma` is the population standard deviation , n is the sample size and
`z_c` is the two-tailed test value for z.

Let x represents the time taken to mail products for all orders received at the office of this company.

As per given , we have

Confidence level : 95%

n= 62

sample mean :
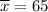`\overline{x}=65` hours

Population standard deviation :
`\sigma=18` hours

z-value for 93% confidence interval:
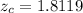`z_c=1.8119` [using z-value table]

Now, 93% confidence the mean time taken to mail products for all orders received at the office of this company :-

`65\pm (1.8119)(18)/(√(62))\\\\ 65\pm4.142\\\\=(65-4.142,\ 65+4.142)\\\\= (60.858,\ 69.142)`

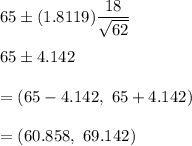
Thus , 93% confidence the mean time taken to mail products for all orders received at the office of this company : (60.858, 69.142)