Question

In a study of the accuracy of fast food​ drive-through orders, one restaurant had 34 orders that were not accurate among 371 orders observed. Use a 0.01 significance level to test the claim that the rate of inaccurate orders is equal to​ 10%. Does the accuracy rate appear to be​ acceptable? Identify the null and alternative hypotheses for this test?

Answer 1

The claim that he rate of inaccurate orders is equal to​ 10% is supported by statistical evidnece at 5% level

Explanation:

Given that in a study of the accuracy of fast food​ drive-through orders, one restaurant had 34 orders that were not accurate among 371 orders observed.

Sample proportion
`p=0.092\\q=1-p = 0.908\\n = 371`

`H_0: p =0.10\\H_a: p \\eq 0.10`

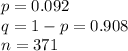
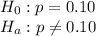
(Two tailed test at 5% significance level)

p difference =
`0.092-0.100\\=-0.0084`

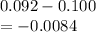
Std error if H0 is true =
`\sqrt{(0.1(0.9))/(371) } \\=0.016`

Test statistic Z = p diff/std error

=0.539

p value = 0.5899

Since p > 0.05 accept null hypothesis

The claim that he rate of inaccurate orders is equal to​ 10% is supported by statistical evidnece at 5% level