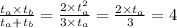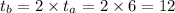Question

person A can paint the neighbors house 2 times as fast as person B. The year A and B work together, it took them 4 days. How long would it take each to paint the house ?

Answer 1

Person A would take 6 days and Person B would take 12 days.

Explanation:

Let
`w` be the work to paint the house.

Let
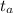`t_(a)` be the time taken by person A to do
`w`.

Let
`t_(b)` be the time taken by person B to do
`w`.

Let
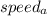`speed_(a)` be the speed of person A to paint.

Let
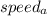`speed_(a)` be the speed of person B to paint.

It is given that person A can paint 2 times as fast as person B.

`speed_(a)=2* speed_(b)`

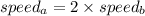
So,person B would take twice time as taken by person A.

`t_(b) =2* t_(a)`

`t_(a)=(w)/(speed_(a))`

`t_(b)=(w)/(speed_(b))`

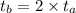
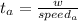
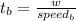
It is given that both of them would take 4 days to paint the house.

`(w)/(speed_(a)+speed_(b))=(w)/((w)/(t_(a))+(w)/(t_(b))) =(t_(a)* t_(b))/(t_(a)+t_(b))`

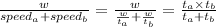
substituting
`t_(b)=2* t_(a)`

Total time to produce=
`(t_(a)* t_(b))/(t_(a)+t_(b))=(2* t_(a)^(2))/(3* t_(a)) =(2* t_(a))/(3)=4`

`t_(a)=6`

`t_(b)=2* t_(a)=2* 6=12`