To solve the problem it is necessary to take into account the concepts related to the Reynolds Number and the Force of drag on the bodies subjected to a Fluid.
The Reynolds number for the Prototype and the Model must therefore be preserved,
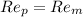
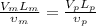
Re-arrange for the speed of the model we have,

Our values at 20°C would be given of the table of Physical Properties of water where

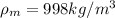
While for the values previous given we have
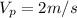

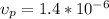
And we have a Ratio between the prototype and the model of 16:1, then

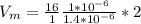
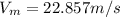
PART B) To calculate the ratio of the drag force now we have to,
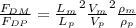
Replacing with our values we have,

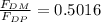
Therefore the ratio of drag force for prototype and model is 0.5016