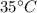Answer:
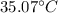
Step-by-step explanation:
To solve this exercise, it is necessary to apply the concepts of Performance Coefficient and work.
For part A, we have given the data on the outside temperature, which is 5°C. In this way the rate of heat loss in the room is given by
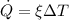
where,
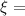 Heat transfer per second
Heat transfer per second
 Change in Temperature
Change in Temperature
We have then,
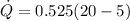
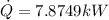
Now we can calculate the coefficient of performance which is given by,
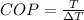
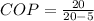
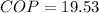
By definition we know that the coefficient of performance of a pump is given by
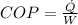
where,
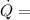 Desired effect
Desired effect
W = Work input
Solving for the work input we have

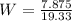
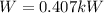
For part B we consider
 as the maximum temperature outside, therefore, calculating the heat rate we have
as the maximum temperature outside, therefore, calculating the heat rate we have
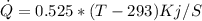
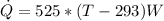
Returning to the expression of the coefficient of performance we have to,
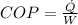
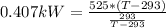
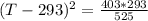
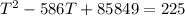
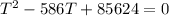
Solving the polynomial you have to
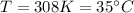
Therefore the maxium outside temperature is