Answer:
70 revolutions
Step-by-step explanation:
t = Time taken
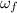 = Final angular velocity
= Final angular velocity
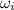 = Initial angular velocity
= Initial angular velocity
 = Angular acceleration
= Angular acceleration
 = Number of rotation
= Number of rotation
Equation of rotational motion
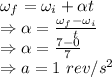
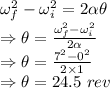
Number of revolutions in the 7 seconds is 24.5
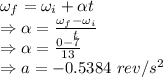
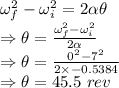
Number of revolutions in the 13 seconds is 45.5
Total total number of revolutions in the 20 second interval is 24.5+45.5 = 70 revolutions