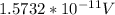Answer:
The maximum emf that can be generated around the perimeter of a cell in this field is
Step-by-step explanation:
To solve this problem it is necessary to apply the concepts on maximum electromotive force.
For definition we know that
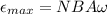
Where,
N= Number of turns of the coil
B = Magnetic field
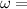 Angular velocity
Angular velocity
A = Cross-sectional Area
Angular velocity according kinematics equations is:
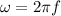
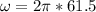
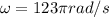
Replacing at the equation our values given we have that
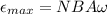
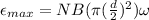
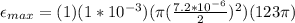
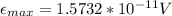
Therefore the maximum emf that can be generated around the perimeter of a cell in this field is