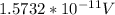Question

Scientific work is currently underway to determine whether weak oscillating magnetic fields can affect human health. For example, one study found that drivers of trains had a higher incidence of blood cancer than other railway workers, possibly due to long exposure to mechanical devices in the train engine cab. Consider a magnetic field of magnitude 0.00100 T, oscillating sinusoidally at 61.5 Hz. If the diameter of a red blood cell is 7.20 µm, determine the maximum emf that can be generated around the perimeter of a cell in this field.

Answer 1

The maximum emf that can be generated around the perimeter of a cell in this field is
`1.5732*10^(-11)V`

Step-by-step explanation:

To solve this problem it is necessary to apply the concepts on maximum electromotive force.

For definition we know that

`\epsilon_(max) = NBA\omega`

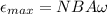
Where,

N= Number of turns of the coil

B = Magnetic field

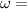`\omega =` Angular velocity

A = Cross-sectional Area

Angular velocity according kinematics equations is:

`\omega = 2\pi f`

`\omega = 2\pi*61.5`

`\omega =123\pi rad/s`

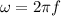
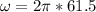
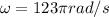
Replacing at the equation our values given we have that

`\epsilon_(max) = NBA\omega`

`\epsilon_(max) = NB(\pi ((d)/(2))^2)\omega`

`\epsilon_(max) = (1)(1*10^(-3))(\pi ((7.2*10^(-6))/(2))^2)(123\pi)`

`\epsilon_(max) = 1.5732*10^(-11)V`

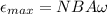
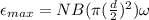
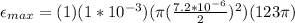
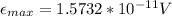
Therefore the maximum emf that can be generated around the perimeter of a cell in this field is
`1.5732*10^(-11)V`