Question

Astrid wants to buy pumpkins and watermelons. She wants to buy more than 10 fruits, and she has a

budget of $117.
P +W > 10 represents the number of pumpkins P and watermelons W Astrid should buy to get more
than 10 fruits.
5.5P +3.5W < 117 represents the number of pumpkins and watermelons she can buy on her budget of
$117.
Does Astrid meet both of her expectations by buying 7 pumpkins and 3 watermelons?

Answer 1

Astrid stays within her budget, but she doesn't buy the expected number of fruits.

Explanation:

I just did it on Khan

Answer 2

Buying 7 pumpkins and 3 watermelons, Astrid doesn't meet her two expectations.

Explanation:

Let

P ----> the number of pumpkins and watermelons she can buy

W ----> the number of watermelons she can buy

we know that

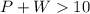`P+W > 10` ----> inequality A

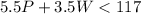`5.5P+3.5W < 117` ---> inequality B

Note Both inequalities are given in the problem

If Astrid buy 7 pumpkins and 3 watermelons

then

we have the ordered pair (7,3)

Remember that

If a ordered pair is a solution of the system of inequalities, then the ordered pair must satisfy both inequalities

For P=7, W=3

Verify Inequality A

`P+W > 10`

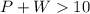
substitute the value of P and the value of W

`7+3 > 10`

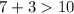
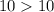`10 > 10` ----> is not true

so

The ordered pair not satisfy the inequality A

Verify Inequality B

`5.5P+3.5W < 117`

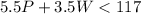
substitute the value of P and the value of W

`5.5(7)+3.5(3) < 117`

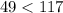`49 < 117` ----> is true

so

The ordered satisfy the inequality B

therefore

Buying 7 pumpkins and 3 watermelons, Astrid doesn't meet her two expectations.