Question

A potter's wheel rotating at 355 rev/min is switched off and rotates through 76.0 revolutions prior to coming to rest. What is the constant angular acceleration of the potter's wheel during this interval? (Assume the positive direction to be the direction of rotation of the wheel. Indicate the direction with the sign of your answer.)________rad/s^2.

Answer 1

-1.44707 rad/s²

Step-by-step explanation:

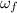`\omega_f` = Final angular velocity

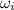`\omega_i` = Initial angular velocity = 355 rpm

`\alpha` = Angular acceleration

`\theta` = Angle of rotation = 76 rps

Converting rpm to rad/s

`1\ rpm=(2\pi)/(60)\ rad/s`

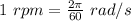
Converting rps to rad/s

`1\ rps=2\pi \ rad/s`

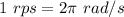
Equation of rotational motion

`\omega_f^2-\omega_i^2=2\alpha \theta\\\Rightarrow \alpha=(\omega_f^2-\omega_i^2)/(2\theta)\\\Rightarrow \alpha=(0^2-355* (2\pi)/(60)^2)/(2* 2\pi * 76)\\\Rightarrow \alpha=-1.44707\ rad/s^2`

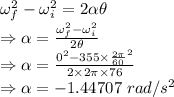
The constant angular acceleration of the potter's wheel during this interval is -1.44707 rad/s²