Step-by-step explanation:
The given data is as follows.
 = 253.4 nm =
= 253.4 nm =
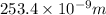 (as 1 nm =
(as 1 nm =
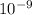 )
)
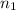 = 5,
= 5,
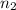 = ?
= ?
Relation between energy and wavelength is as follows.
E =

=
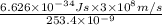
=
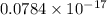 J
J
=
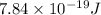
Hence, energy released is
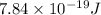 .
.
Also, we known that change in energy will be as follows.
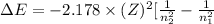
where, Z = atomic number of the given element

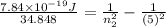
0.02 + 0.04 =
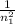
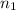 =
=
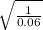
= 4
Thus, we can conclude that the principal quantum number of the lower-energy state corresponding to this emission is n = 4.