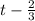Answer:
Explanation:
The average (arithmetic mean) length per film for a group of 21 films is t minutes
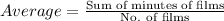
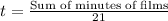
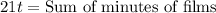
A film that runs for 66 minutes is removed from the group and replaced by one that runs for 52 minutes
So,
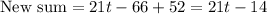
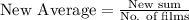
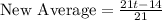

Hence the average length per film, in minutes, for the new group of films, in terms of t is