Question

Assume that the car lot contains 40 percent BMWs, 25 percent Volvos, and 35 percent Jaguars. Of the BMWs, 90 percent have navigation systems, 30 percent of the Volvos have navigation systems, and 50 percent of the Jaguars have navigation systems. You are assigned a car at random. If the car has a navigation system, what is the probability that it is not a BMW?

Answer 1

The required probability is 0.4098.

Explanation:

Consider the provided information.

According to conditional probability that A occurs , given B has occurred.

`P(A|B)=(P(A\cap B))/(P(B))`

Assume that the car lot contains 40 percent BMWs, 25 percent Volvos, and 35 percent Jaguars.

Pr(BMWs)=0.40

Pr(Volvos)=0.25

Pr(Jaguars)=0.35

Of the BMWs, 90 percent have navigation systems, 30 percent of the Volvos have navigation systems, and 50 percent of the Jaguars have navigation systems.

Pr(Navigation | BMWs)=0. 90

Pr(Navigation l Volvos)=0.30

Pr(Navigation l Jaguars)=0.50

Total cars with navigation system = 0.40×0.90+0.25×0.30+0.35×0.50

=0.36+0.075+0.175=0.61

Pr(Not Bmw l Navigation system) =
`(0.25*0.30+0.35*0.50)/(0.61)\approx0.4098`

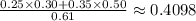
Hence, the required probability is 0.4098.