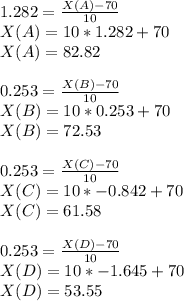Question

The numerical course grades in a statistics course can be approximated by a normal model with a mean of 70 and a standard deviation of 10. The professor must convert the numerical grades to letter grades. She decides that she wants 10% A's, 30% B's, 40% C's, 15% D's, and 5% F's.

What is the cutoff for an A grade?
What is the cutoff for an B grade?
What is the cutoff for an C grade?
What is the cutoff for an D grade?

Answer 1

A = 82.82

B = 72.53

C = 61.58

D = 53.55

Explanation:

First, determine the percentile at which the cutoff grade in each letter grade interval falls on and find the equivalent z-score:

A: (100-10) = 90-th percentile

z-score = 1.282

B: (100-10-30) = 60-th percentile

z-score = 0.253

C : (100-10-30-40) = 20-th percentile

z-score = -0.842

D: (100-10-30-40-15) = 5-th percentile

z-score = −1.645

The value 'X' for each cutoff can be found by applying the z-score equation:

`z= (X- \mu )/(SD)`

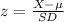
Where μ is the mean and SD is the standard deviation

Therefore, the cutoffs are:

`1.282= (X(A)- 70)/(10)\\X(A) = 10*1.282 +70\\X(A) = 82.82\\\\0.253 = (X(B)- 70)/(10)\\X(B) = 10*0.253 +70\\X(B) = 72.53\\\\0.253 = (X(C)- 70)/(10)\\X(C) = 10*-0.842 +70\\X(C) = 61.58\\\\0.253 = (X(D)- 70)/(10)\\X(D) = 10*-1.645 +70\\X(D) = 53.55\\`