3
Explanation:
The equation of line passing through the two points is

When substituted,the equation becomes
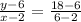
which when simplified is
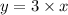
The line clearly passes through origin.
The distance between two points is
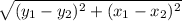
Distance between origin and
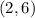 is
is
 .
.
Distance between origin and
 is
is
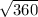
Scale factor is
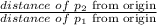
So,scale factor is
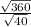
which when simplified becomes 3.